
一、空间曲线的一般方程
导入:在立体几何中,我们学过:两平面相交,交于一条直线。
空间直线C可看作空间两曲面的交线。
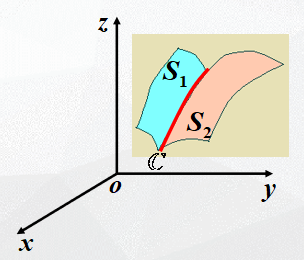
空间曲线的一般方程
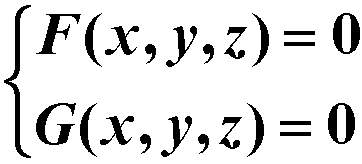
例1:方程组x^2+y^2+z^2=25和z=3表示以O为球心,半径为5的球面与z=3平面的交线。
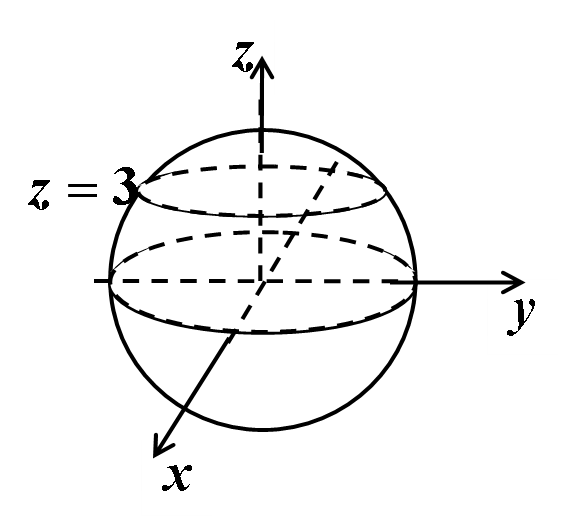
交线为圆
特点:曲线上的点都满足方程,满足方程的点不能同时满足两个方程。
例2:方程组x^2+y^2=16,z=3表示怎样的曲线?
交线为圆
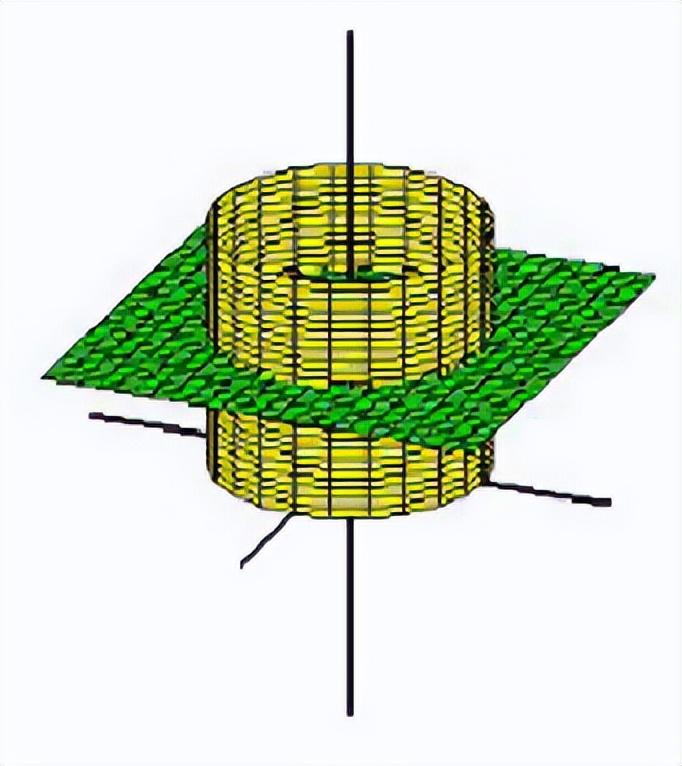
例3 方程组
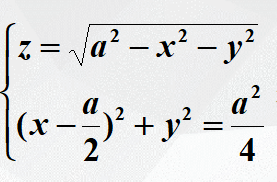
表示怎样的曲线?
解:

表示上半球面,
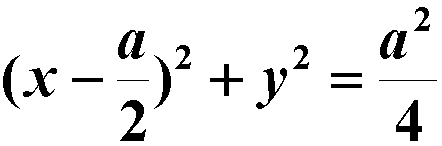
表示圆柱面
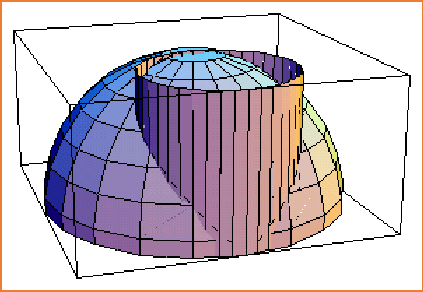
交线如图:维维安妮曲线
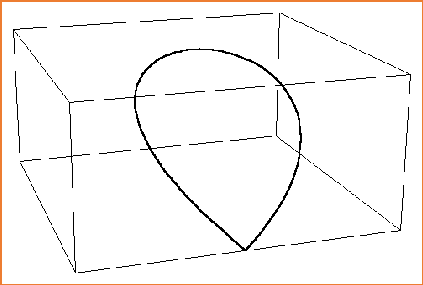
二、空间曲线的参数方程
空间曲线的参数方程如下
x=x(t) y=y(t) z=z(t) (α <=t<=β )
显然C上动点的坐标x,y,z都表示为参数t的函数,t=t1对应C上的一点t,t从α 连续变到 β时,可得到C上的全部点。
例4:若空间一点M在圆柱面x^2+y^2=a^2上以角速度w绕z轴旋转,同时又以线速度v沿平行于z轴的正向上升(其中w、v都是常数),则点M的轨迹构成螺旋线,试建立其参数方程。
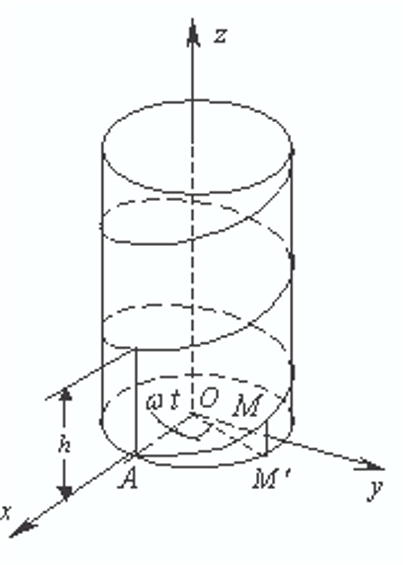
解:取时间t为参数,设t=0时,动点位于A(0,0,0)处,经过时间t,动点由A移动到M(x,y,z),M在xoy面上的投影M'(x,y,0)
由于动点在圆柱上以角速度w绕z轴旋转,经过时间t,角AOM'=wt
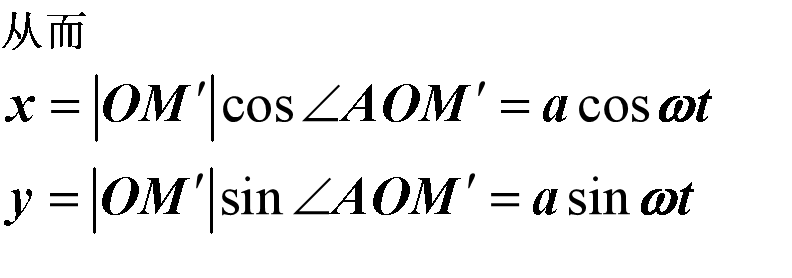
动点以线速度v沿平行于z轴的正方向上z=M'M=vt
因此螺旋线的参数方程为x=acoswt,y=asinwt,z=vt
三、在坐标轴上的投影
1、平面曲线在坐标轴上的投影
2、平面区域在坐标轴上的投影
3、有向曲线在坐标轴上的投影
四、在坐标面上的投影
1、空间曲线在坐标面上的投影
设空间曲线的一般方程
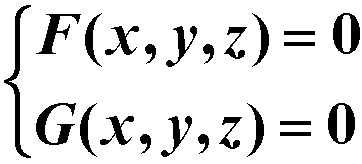
在xoy平面上的投影
设空间曲线的一般方程:F(x,y,x)=0 G(x,y,z)=0
消去变量z后得:H(x,y)=0
空间曲线关于xoy面的投影柱面
投影柱面的特征:以此空间为准线,垂直于所投影的坐标面。

例5 求曲线x^2+y^2+z^2=1和z=1/2 在xoy坐标面上的投影。

解:消去变量z后得x^2+y^2=3/4,
在xoy面上的投影为x^2+y^2=3/4 z=0
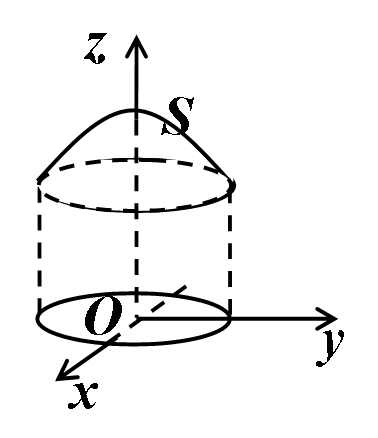
例6 求抛物面y^2+z^2=x 与平面x+2y-z=0的截线在三个坐标面上的投影方程。
解:截线方程为y^2+z^2=x x+2y-z=0
如图
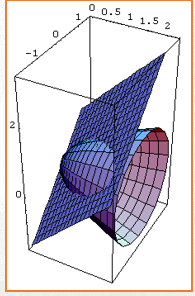
(1)消去z得投影x^2+5y^2+4xy-x=0 z=0
(2)消去y得投影x^2+5z^2-2xz-4x=0 y=0
(3)消去x得投影y^2+z^2+2y-z=0 x=0
补充:空间立体或曲面在坐标面上的投影.
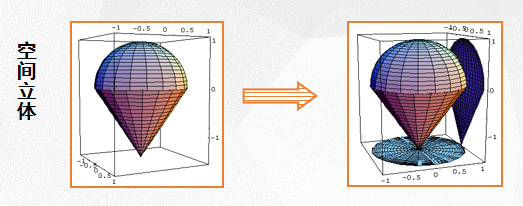
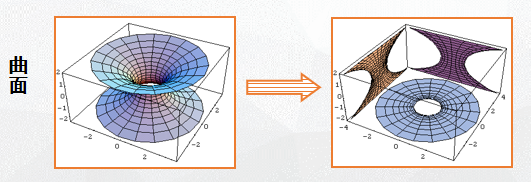
例7:

则交线C在xoy面上的投影为x^2+y^2=1 z=0一个圆
所求立体在xoy面上的投影为
x^2+y^2<=1